1. INTRODUCCIÓN A LA CINEMÁTICA.
2. MAGNITUDES CINEMÁTICAS
A. TRAYECTORIA
B. DESPLAZAMIENTO
C. VELOCIDAD
D. ACELERACIÓN
3. CLASIFICACIÓN DE LOS MOVIMIENTOS:
A. MRU
B. MRUA
C. MCU
1. INTRODUCCIÓN A LA CINEMÁTICA.
La Cinemática (del griego, kineo, movimiento) es la parte de la Mecánica que estudia el movimiento sin tener en cuenta las causas que lo producen.
Un cuerpo está en movimiento si cambia su posición en el espacio con respecto a un determinado Sistema de Referencia (O) que normalmente se considera fijo.
Un cuerpo está en reposo si su posición respecto a un Sistema de Referencia no cambia durante el transcurso de, otra magnitud fundamental e importante en cinemática, el tiempo.
Por tanto, es importante para describir un movimiento indicar respecto a qué sistema de referencia se han tomado las medidas:
No es lo mismo describir el movimiento de un coche observado desde la acera mientras esperamos para cruzar un paso de peatones, que respecto a otro coche que lo está adelantando, ¿verdad?
No es lo mismo describir el movimiento de un coche observado desde la acera mientras esperamos para cruzar un paso de peatones, que respecto a otro coche que lo está adelantando, ¿verdad?
Concluímos que tanto el reposo como movimiento son conceptos relativos ya que dependen del sistema de referencia que tomemos.

2. MAGNITUDES CINEMÁTICAS o las propiedades que describen el movimiento.
Magnitud es toda aquella propiedad de un cuerpo o fenómeno que puede ser medida. En cinemática, además de la magnitud fundamental tiempo, utilizaremos:
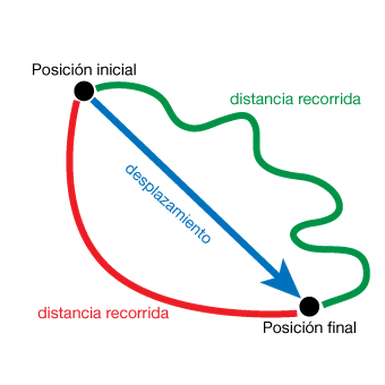
- La magnitud fundamental LONGITUD aparece implícita en el DESPLAZAMIENTO y la TRAYECTORIA, ¡que no son lo mismo!
- Dos magnitudes derivadas: la VELOCIDAD y la ACELERACIÓN, que además son magnitudes vectoriales; es decir, dependen del sentido y de la dirección del movimiento.
¿Qué es un vector?
Como has visto, muchas magnitudes cinemáticas son vectoriales (el vector desplazamiento, la velocidad y la aceleración). Un vector no es más que una herramienta matemática muy utilizada y necesaria en Física. Un vector es un segmento orientado (similar a una flecha) se suele representar con una letra minúscula o dos mayúsculas (origen y final) con una flecha arriba. En un vector se distinguen las siguientes componentes:
A. TRAYECTORIA.
Depende del Sistema de Referencia elegido para estudiar el movimiento. Se denomina trayectoria al camino seguido por el cuerpo estudiado durante su movimiento.
El espacio (S) que recorre un cuerpo en su movimiento se define como la longitud de la trayectoria recorrida. Se mide en metros.
Definamos::
- POSICIÓN: lugar que ocupa el móvil en un instante respecto al sistema de referencia.
- MÓVIL: Es el cuerpo cuyo estado de reposo o movimiento se está estudiando.
B. VECTOR DESPLAZAMIENTO (Δx).
Es la distancia que existe entre dos puntos del recorrido en el sentido del movimiento. Solo coincide con la trayectoria cuando el movimiento es rectilíneo.
EJERCICIO 1: Un móvil en un instante determinado se encuentra en la posición (1,6), unos segundo más tarde, pasa a ocupar la posición determinada por el punto (3,7), determina cuál es su desplazamiento y su trayectoria.
C. VELOCIDAD (v).
(Del vídeo interesa solo la primera parte, usa otras letras en la fórmula de rapidez y no define velocidad como desplazamiento entre tiempo. Omitamos los grados, se refiere al sentido del vector desplazamiento)
La velocidad es la magnitud física que estudia la variación de la posición de un cuerpo en función del tiempo respecto a un determinado sistema de referencia. En el SI sus unidades son m/s; aunque también se puede expresar de otras formas en función del móvil en estudio: km/h, cm/s, etc.
Distingamos entre velocidad media y velocidad instantánea.
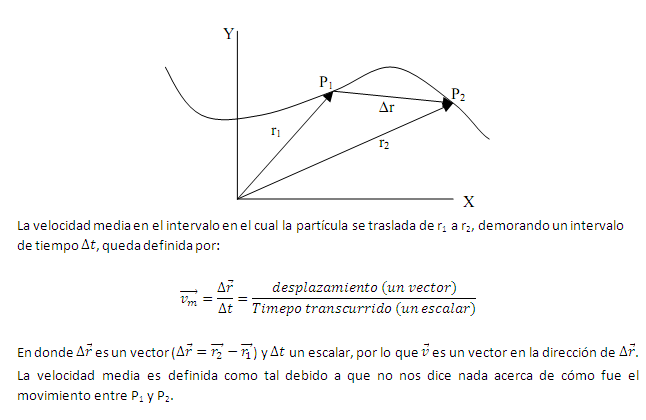
- VELOCIDAD MEDIA:
Supongamos un móvil (representado por un punto) que se ha desplazado del punto 1 (P1) al 2 (P2) describiendo la siguiente trayectoria:
También se puede calcular la velocidad media respecto de la trayectoria S. En algunos libros la llaman celeridad o rapidez y se calcula dividiendo el espacio recorrido entre el tiempo que el móvil ha tardado en recorrerlo.
- VELOCIDAD INSTANTÁNEA:
Es la velocidad que nos indicaría un velocímetro, es decir, la velocidad en ese mismo instante.
Para saber más:
Nota: En 1º Bachillerato contemplarás su tratamiento vectorial
Concluimos que la velocidad es un vector cuya dirección y sentido coinciden con los del vector desplazamiento.
EJERCICIO 2: Calcula el espacio que recorre un móvil que se desplaza con velocidad constante de 15 m/s durante 20 s
Se define como la variación de la velocidad respecto al tiempo. Su unidad en el SI suele ser m/s2.
Existe aceleración siempre que la velocidad de un cuerpo cambia ya sea porque:
- Aumenta su velocidad (acelera)
- Disminuye su velocidad (frena)
- Cambia de dirección (gira)
EJERCICIO 3: Calcula la aceleración de un coche que va con una velocidad de 80 km/h y pasa a 120 km/h en 8 segundos.
No te habrá costado mucho llegar a su expresión matemática o fórmula:
- ACELERACIÓN MEDIA: Estudia el cambio de velocidad en un intervalo de tiempo.

- ACELERACIÓN INSTANTÁNEA:

EJERCICIO 4: Un cuerpo que va con una velcidad de 4 m/s frena de repente con una aceleración de 0,5 m/s2 calcula cuanto tiempo tarda en detenerse.
2. CLASIFICACIÓN DE LOS MOVIMIENTOS
CRITERIOS:
1.- Según la trayectoria:
- Rectilíneos: su trayectoria es una línea recta
- Curvilíneos: su trayectoria no es recta. Se incluyen aquí el movimiento circular y el ondulatorio.
2.- Según la velocidad:
- Uniforme: el valor de la velocidad no cambia.
- Variados (no uniformes porque su velocidad aumenta o disminuye, acelerado o desacelerado).
Existen:
- Movimientos sin aceleración (aclaro: debida al cambio del valor de la velocidad): Movimientos uniformes (MRU, MCU)
¡OJO! En el MCU existe aceleración debida al cambio de la dirección del vector velocidad
¡OJO! En el MCU existe aceleración debida al cambio de la dirección del vector velocidad
- Movimientos con aceleración constante: Movimientos acelerados (MRUA, la caída libre)
A. M.R.U.: Movimiento Rectilíneo Uniforme.
- La trayectoria es una línea recta.
- Su velocidad es constante. Además, su velocidad no cambia de dirección por lo que no existirá aceleración normal.
Ecuaciones: v = cte
x(t) = x 0 + v t; donde x0 es la posición inicial e indica la distancia desde el origen.
Gráficas:
La gráfica x-t es una línea recta. La inclinación (pendiente) nos da la velocidad. El punto de corte con el eje vertical da x0
EJERCICIO 5: Piensa en tres ejemplos para cada uno de los casos de las gráficas anteriores.
EJERCICIO 6: ¿Por qué decimos que cuanto mayor pendiente en la gráfica x-t mayor velocidad?
- La trayectoria es una recta
- La aceleración es constante
Como vimos, la aceleración mide la rapidez con la que varía la velocidad. Se mide en m/s2. Así, una aceleración de 5 m/s2 indica que la velocidad aumenta a razón de 5 m/s cada segundo.
Llamaremos indistintamente MRUA tanto a los movimientos acelerados como los desacelerados. Desde el punto de vista físico, la única diferencia que existe entre ellos es el sentido del vector aceleración.
Ecuaciones:
v(t) = v0 + a t
x(t) = x0 + v0 t + ½ a t 2
Donde:
v0 = velocidad cuando t =0
x0 = distancia al origen cuando t =0
x(t) = distancia al origen (puede que no coincida con el espacio recorrido). Depende del tiempo (variable independiente)
t = 0, significa cuando empieza a contarse el tiempo o cuando se aprieta el cronómetro
El signo de la aceleración y de la velocidad depende del sistema de referencia que tomemos, no de que el cuerpo acelere o frene. Si consideramos positivo el sentido de avance del cuerpo una aceleración es negativa si va en contra del avance del cuerpo y positiva si va a su favor.
Por tanto, un cuerpo frena si su aceleración va en sentido contrario de la velocidad y acelera si ambas van en el mismo sentido.
Lo normal es tomar el sentido positivo como el sentido positivo del eje X (cuando el movimiento es en una sola dimensión, claro).
EJERCICIO 7: Interpreta las siguientes gráficas.
EJERCICIO 8: Se habla de caída libre cuando estudiamos como caen los cuerpos en la Tierra por efecto de la aceleración de la gravedad, ¿cómo cambiarían las ecuaciones de ese caso particular de MRUA?
En el siguiente enlace puedes repasar las gráficas de los distintos tipos de movimientos
C. M.C.U.: Movimiento Circular Uniforme.
Los movimientos circulares están muy presentes en nuestro entorno: el movimiento de las ruedas de un coche, los engranajes, un ventilador, el movimiento de la tierra, etc.
Los movimientos circulares se pueden estudiar con magnitudes lineales (como hemos visto hasta ahora), pero también existen magnitudes angulares.
- La trayectoria es una circunferencia.
- La velocidad es constante.

a) midiendo el ángulo girado o
b)el arco de circunferencia recorrido en un intervalo de tiempo?
El vector aceleración tiene por tanto 2 componentes:
a) La aceleración tangencial, con misma dirección y sentido que la velocidad.
b) La aceleración centrípeta o normal, dirigida hacia el centro de la circunferencia
descrita por el movimiento.
*El período se mide en Hz o s-1
EJERCICIO 9: ¿Coinciden su desplazamiento y su trayectoria? Explícalo.
No coinciden porque la trayectoria es un circunferencia. Imaginad una noria en movimiento, pasado cierto tiempo vuelves a estar en la misma posición. Para un observador que esté en tierra (fuera del movimiento) y que deje de mirar y vuelva a mirar de nuevo, puede parecerle que no ha existido movimiento alguno.
EJERCICIO 10:
A) Dos amigos suben en un tiovivo. uno se sienta en un elefante situado a 5 m del centro, y otro escoge un coche de bomberos situado a sólo 3,5 m del centro. Ambos tardan 4 min en dar 10 vueltas. a) ¿Se mueven con la misma velocidad lineal? ¿Y con la misma velocidad angular? Razónalo. b) Calcula las velocidades lineal y angular de ambos.
B) La rueda de una bicicleta tiene 30 cm de radio y gira uniformemente a razón de 25 vueltas por minuto. Calcula: a) La velocidad angular, en rad/s. b) La velocidad lineal de un punto de la periferia de la rueda.