TEORÍA DE LOS
ERRORES
Las medidas de las magnitudes físicas se realizan con instrumentos de medida. Los instrumentos de medida tienen varias cualidades:
a) INTERVALO DE MEDIDA: es el conjunto de valores que un instrumento puede medir. Va desde el valor mínimo al valor máximo.
b) SENSIBILIDAD de un aparato de medida es la respuesta del instrumento de medida a las variaciones de la magnitud que mide. Es decir, es la mínima medida que el aparato puede apreciar en su escala (umbral mínimo).
Ej: Si tenemos un termómetro que va de 0,5ªC en 0,5ºC y queremos medir la temperatura de un clase, no podemos decir que la temperatura de la clase sea 27,3ºC. Diríamos que es 27,0 ºC o 27,5ºC. ¿Cómo expresaríamos el resultado de la medida?
27,5 +- 0,5 ºC ,lo cual indica que existe una gran probabilidad de que la medida está entre 27 y 28 grados Celsius.
¿Cuál es el intervalo de medida (la cota inferior y la superior) y la sensibilidad del siguiente termómetro?
Intervalo: desde 35 a 42 ºC. Sensibilidad: 0,1 ºC
Medir lleva implícito
cometer errores, por lo que existe incertidumbre en la medida. Se habla de dos tipos de
errores:
a) Errores sistemáticos.
Se cometen debido al mal calibrado del aparato de medida o a la persona que
efectúa la medida.
b) Errores aleatorios o
accidentales. Son debidos al azar, fortuitos e imprevisibles. Por ejemplo, un cambio en otra variable (temperatura). Se minimizan realizando muchas mediciones.
- Precisión: se refiere a como concuerdan entre sí medidas de una misma magnitud.
- Exactitud: indica lo próximas que están las medidas individuales tomadas al valor real.
Cálculo de error
absoluto y error relativo.
- El error absoluto (Ea) es la diferencia entre el valor medido y el valor real o verdadero, que como no conocemos representamos con la media.
- El error relativo (Er) es el error cometido entre unidad de lo medido (divido error absoluto y valor estimado -media-). Es adimensional. Por cien nos informa del porcentaje de error.
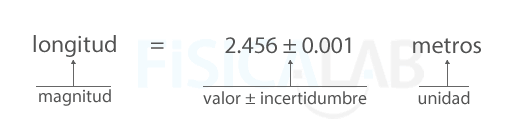
Expresión correcta de una medida:
Ejemplo: Las
masas de sulfato de cobre CuSO4 medidas en el laboratorio
con una balanza son:
3,51
g 3,48 g 3,49g 3,52 g 3,48 g
Calcula el error absoluto medio y el relativo medio.
1º
. Debemos elegir un valor que nos represente a esos datos: la media
aritmética (valor estimado o esperado) VE = 3, 496
g
redondeo
3,50 g
2º. Completemos la siguiente tabla.
Medida (g)
|
Error absoluto (g)
|Valor – VE|
|
Er = Ea/VE
|
3,51
|
|3,51- 3,50|= 0,01
|
Error relativo medio = 0,02/3,5
= 0,0057 (no tiene unidades)
%error = 0,0057*100= 0,57% de error
|
3,48
|
|3,48 – 3,50|=|- 0,02|
|
3,49
|
|3,49 – 3,50|= |- 0,01|
|
3,52
|
|3,52 – 3,50|= 0,02
|
3,48
|
|3,48 – 3,50|=|-0,02|
|
|
Media = 0,016 =0,02, gramos
|
La correcta expresión de la medida sería 3,50 +- 0,02 g
ACTIVIDADES:
1) Con un cronómetro analógico con sensibilidad de 1 s mides 0,45 minutos. ¿Cuántos segundos son? Expresa la medida con su incertidumbre y calcula su error relativo.
2) Explica la diferencia entre precisión y exactitud.
3) Medimos la masa de dos cuerpos, si un cuerpo tiene de masa 5 kg ± 0,02 kg y otro de 0,09 kg ± 0,0021 kg, determinar en cuál de los dos se produce mayor error.
4) En una carrera de atletismo se obtienen los siguientes resultados en la prueba de 50 metros: 7,85 ; 7,84 ; 7,85 ; 7,85 y 7,86 (segundos). Calcula el error absoluto, el error relativo medio y expresa la medida de forma correcta.
5) En el siguiente cuadro se muestran los resultados de las mediciones de una longitud dada:
Medición
|
Medida
|
N°
|
cm
|
1
2
3
4
5
6
7
|
2,83
2,85
2,87
2,84
2,86
2,84
2,86
|
Calcula el valor estimado, el error absoluto y el relativo (medios). Expresa la medida resultante de forma correcta.
THEORY OF ERRORS
Measurements of the physical quantities are made with measuring instruments. The measuring instruments have properties:
a) MEASUREMENT INTERVAL from minimum to maximum value. The RANGE is the difference between the minimum value and the maximum value that a device can measure.
b) SENSITIVITY of a measuring device depends on the smallest division of the scale (minimun threshold). So, it is the response of the measuring instrument to the variations of the magnitude which is measuring.
Example: If we have a thermometer with minimun threshold of 0,5ªC and we want to measure the temperature of a class, we cannot say that the temperature of the class is 27,3ºC. We would say: 27.0ºC or 27.5ºC. How to express the result of the measure?
27.5 +- 0.5 ºC, which indicates that we are sure that the measurement is between 27 and 28 Celsius degrees.
What are the minimum and maximum value, the measurement interval, the range and the sensitivity of the following thermometer?

Interval: from 35 to 42 ºC. Sensitivity: 0,1 ºC
Page 7: 1,2 y 3 (IN FOCUS)
Measurements are accompanied by errors. We can distinguish between two types of errors:
a) Systematic errors which can be due to the equipment and how it is used. For example, they are committed due to poor calibration of the measuring device or to the person who is measuring. They are avoidable.
b) Random or accidental errors which are due to unpredictable causes, so they are unavoidable. For example, a change in one variable (temperature). However, they could be minimized by making many measurements.
ACCURACY AND PRECISION.
In sciences, it is important to distinguish between precision and accuracy.
ACCURACY: Accuracy indicates how close the individual measurements are to the real value.
PRECISION: Precision refers to how measurements of the same magnitude agree with each other.
See the difference between accurate and precise measurements in the bull’s eye figure below. Scientists want measurements that are both accurate and precise…

ABSOLUTE AND RELATIVE ERROR CALCULATION.
Absolute error and relative error are two types of experimental error. Before calculating, it is good to understand the difference between them.
a) Absolute error is a measure of how far 'off' a measurement is from a true value. It is an indication of the uncertainty in a measurement. For example, if you measure the width of a book using a ruler with millimeter marks, the best you can do is measure the width of the book to the nearest millimeter. You measure the book and find it to be 75 mm. You report the absolute error in the measurement as 75 mm +/- 1 mm. The absolute error is 1 mm. Note that absolute error is reported in the same units as the measurement.
Alternatively, you may have a known or calculated value and you want to use absolute error to express how close your measurement is to the ideal value. Here absolute error is expressed as the difference between the expected and actual values.
Absolute Error = /Measured Value - Real Value*/
* Real value is unknown so we calculate the arithmetic average.
For example, if you know a procedure is supposed to yield 1.0 liters of solution and you obtain 0.9 liters of solution, your absolute error is /0.9 - 1.0/ = 0.1 liters.
b) Relative error. Relative error expresses how large the absolute error is compared with the total size of the object you are measuring. Relative error is expressed as a fraction or is multiplied by 100 and expressed as a percent.
Relative Error = Absolute Error / Known Value*
* Known value is the arithmetic average
For example, a driver's speedometer says his car is going 60 kilometre per hour (km/h) when it's actually going 62 km/h. The absolute error of his speedometer is /62 - 60/ = 2 km/h. The relative error of the measurement is 2 km/h / 60 km/h = 0.033 or 3.3%
Example: The CuSO4 copper sulfate masses measured in the laboratory with a balance are: 3.51 g , 3.48 g, 3.49 g, 3.52 g , 3.48 g and 5.25 g. Calculate the absolute error and the relative error which have been comitted in measuring.
(Average absolute and relative errors).
ACTIVITIES:
1) Using an analog chronometer whose sensitivity is 1 s, you have measured 0.45 minutes. How many seconds are? Express the measurement with its uncertainty and calculate its relative error.
(Average absolute and relative errors).
2) Explain the difference between precision and accuracy.
3) We measure the mass of two bodies:
body 1: 5 kg ± 0.02 kg
body 2: 0.09 kg ± 0.0021 kg
Determine in which of them a greater error have been committed.
4) The following results have been obtained in an athletics race. Spent time in 50-meter test: 7.85; 7.84; 7.85; 7.85 and 7.86 (seconds). Calculate the average absolute error, the average relative error and express the average representative measurement correctly.
5) The following table shows the results of measuring length (in centimetre):
Trial
|
Length
|
Number
|
cm
|
1
2
3
4
5
6
7
|
2,83
2,85
2,87
2,84
2,86
2,84
2,86
|
Calculate the absolute error, the relative error and express the average representative measurement properly.